Structured Uncertainty

Ivor Simpson
University of Sussex

Sara Vicente
Niantic

Neill D.F. Campbell
University of Bath

This page presents our ongoing work on modelling structured uncertainty for computer vision tasks. We introduce our Structure Uncertainty Prediction Network (SUPN) model published at CVPR 2018 working with Era Dorta and Lourdes Agapito.

Structured Uncertainty Prediction Networks

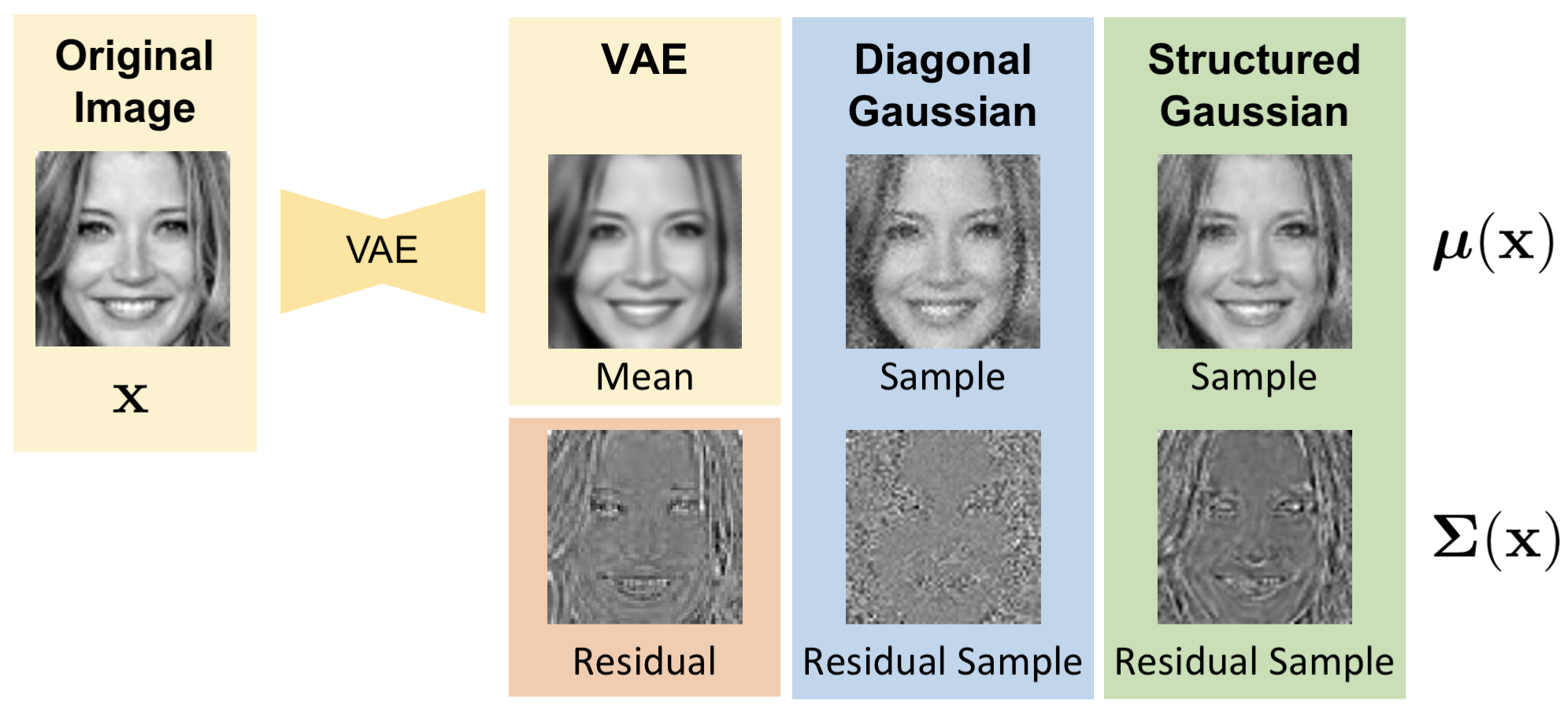
**An overview of the SUPN model.** The output of a VAE fails to capture image details that are observed in the residual image. We can see that the residual image displays structure (correlations between the pixels). The common use of a diagonal loss or log-likelihood in the VAE treats these errors as independent; the resulting samples fail to capture the structure in the residual. In constrast, the structured likelihood used for SUPN is able to capture this structure and the resulting samples display the same statistics as the original input image.

The figure provides an overview of our Structured Uncertainty Prediction Networks (SUPN) model. Consider a Variational Auto-Encoder (VAE) as a deep generative model. The reconstruction obtained from a VAE is often overly smooth due to the limitations of the architecture (e.g. latent space dimensionality) and the loss function used (e.g. Mean Squared Error or L2). We can consider the loss function as the log of the likelihood function over the observed data, thus the VAE predicts a distribution over the observed data. An L2 loss is the equivalent of a spherical Gaussian distribution with a single variance across all pixels.

To improve quality, it is common to estimate a diagonal distribution where we predict a different variance for each pixel. This is shown in the middle column. If we look at the residual between the mean VAE reconstruction and the original image (orange box) we can see that structure remains in the residual. The diagonal model fails to capture this structure; as a result, the error is estimated independently per pixel resulting in noisy samples that fail to reflect the original image statistics. In contrast, the SUPN model captures the structure in the error such that samples drawn are found to match the statistics of the residual and thus the original input.

Please see below for a section of a talk given at the BMVA workshop on generative models that discusses the SUPN model (PDF of slides):

Learning Structured Gaussians to Approximate Deep Ensembles

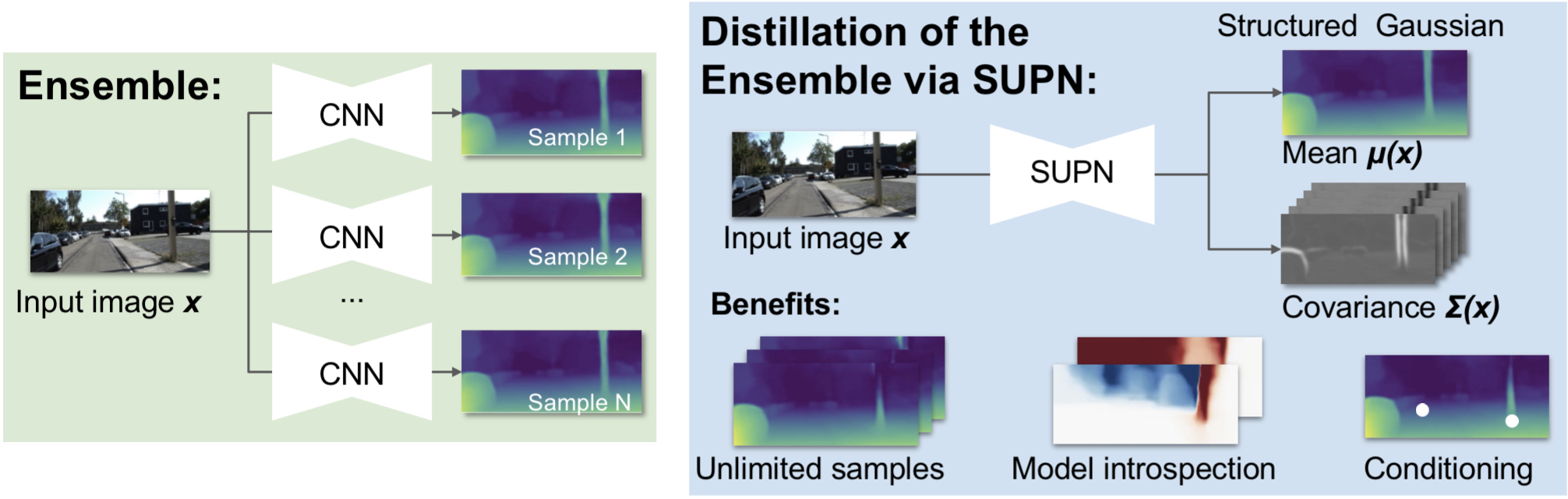
**Using the SUPN model to approximate the output of a deep ensemble.** We learn an structured Gaussian distribution to approximate the output from a pre-trained deep ensemble for the task of monocular depth estimation from [Poggio et. al. CVPR 2020]. This explicit distribution captures the uncertainty in the prediction and, in addition to providing improved efficiency, enables a variety of tasks including: sampling, conditioning and model introspection.

This work builds on our SUPN model to provide a closed-form approximator for the output of probabilistic deep ensembles used for dense image prediction tasks. Similarly to distillation approaches, the single network is trained to maximise the probability of samples from pre-trained probabilistic models, in the paper we use a fixed ensemble of networks. Once trained, this compact representation can be used to draw efficiently spatially correlated samples from the approximated output distribution. Importantly, this approach captures the uncertainty and structured correlations in the predictions explicitly in a formal distribution, rather than implicitly through sampling alone. This allows direct introspection of the model, enabling visualisation of the learned structure. Moreover, this formulation provides two further benefits: estimation of a sample probability, and the introduction of arbitrary spatial conditioning at test time. We demonstrate the merits of our approach on monocular depth estimation and show that the advantages of our approach are obtained with comparable quantitative performance.

Publications

VAEs with Structured Image Covariance Applied to Compressed Sensing MRI,
Margaret Duff, Ivor Simpson, Matthias J. Ehrhardt and Neill D. F. Campbell,
IoP Physics in Medicine and Biology, vol. 68, no. 16, 2023
[pdf] [arXiv link] [DOI: 10.1088/1361-6560/ace49a]

Learning Structured Gaussians to Approximate Deep Ensembles,
Ivor Simpson, Sara Vicente and Neill D. F. Campbell,
IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), 2022
[pdf] [supplemental]

Cell Anomaly Localisation using Structured Uncertainty Prediction Networks,
Boyko Vodenicharski, Samuel McDermott, Katherine Webber, Viola Introini, Pietro Cicuta, Richard Bowman, Ivor Simpson and Neill D. F. Campbell,
Int. Conf. on Medical Imaging with Deep Learning (MIDL), 2022
[pdf] [code]

Structured Uncertainty Prediction Networks,
Era Dorta Perez, Sara Vicente, Lourdes Agapito, Neill D. F. Campbell and Ivor Simpson,
IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), 2018
[pdf] [supplemental] [code]

Acknowledgements

This work has been supported by EPSRC CDE (EP/L016540/1) and CAMERA (EP/M023281/1) grants as well as the Royal Society.